movimiento circular
Movimiento circular uniforme
1 radian=57.3 grados
Velocidad angular = Δξ --------angulo girado
Δt -------- tiempo empleado
Formulas de mcu
W=ɸ/t
W=Δɸ=ɸ2-ɸ1
Δt t2-t1
w=2pi rad =2pi para radianes
t t
w=2pi f
wm=wf-w0
2
F=1/t
W=velocidad angular
ɸ=movimiento angular
t=tiempo
f=frecuencia
Movimiento circular uniforme
ɸ=w0t +at2
2
ɸ=wf2-w02
2 a
ɸ=wf-w0 t
2
|
ɸ=at2/2 ɸ=wf2 2 a
ɸ=wf t 2 |
|
Cuando el cuerpo está en reposo y w0 es cero |
Leyes de newton
Primera ley de newton
Se llama ley de la inercia que dice que cualquier objeto quiere estar en reposo o en movimiento y esto cambia solo que se le aplique una fuerza.
Segunda ley de newton
El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza imprime.
La fuerza se detiene simplemente en función del momento en que se aplica a un objeto.
Masa > fuerza= aceleración <
Masa < fuerza =aceleración >
Tercera ley de newton
Con toda acción ocurre siempre una reacción igual y contraria: ósea, las acciones mutuas de dos cuerpos siempre son iguales y dirigidos en sentido opuesto.
|
A=v/t---si le velocidad inical es cero M=w/g---peso M=w/g |
Formulario
F=ma
M=f/a
A= f/m
M=p/g
F=p/g (a)
A=vf-vi/t
P=mg
R=mg--- reaccion
Equilibrio traslacional
Un cuerpo se encuentra en equilibrio traslacional cuando la sumatoria de todas los componentes en (x) es igual a cero al igual que en (y),.

Equilibrio traslacional
2 niños sostienen una piñata cuyo peso es de 196 N formando un angulo de 140 grados con ambas cuerdas.
Calcular la fuerza que ejerce cada niño.
Se sacan componentes.
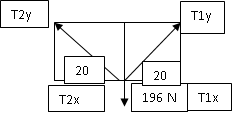
|
Sen 20°=cy2/t2 Cy2=t2 sen 20° Cos 20°=cx2/t2 Cx2=-t2 cos 20°
|
|
sen 20°=cy1/t1 cy1=t1 sen 20° cos 20°=cx1/t1 cx1=t1 cos 20°
|
Ifx=-cx2+cx1=0
-t2 cos 20°
Ti cos 20° =0
-0.93 t2+ 0.93 t1=0
Ify=t2 sen 20° + ti sen 20°-196 =0
T2 sen 20° + t1 sen 20°=196
0.34 t2 +0.34 t1=196
T1=t2=t
0.34t +0.34 t=196
0.68 t=196
T=196/0.68
T1=288.24 N
T2=288.24 N
Equilibrio rotacional
Una barra uniforme de 100m de longitud y de 60 kg de peso está sometida a la acción de una fuerza hacia arriba de 50kg aplicada en un punto de 20 cm de un punto A y a la fuerza vertical hacia debajo de 60 y 30 kg en A y B respectivamente .hayas el equilibrante y su punto de aplicación
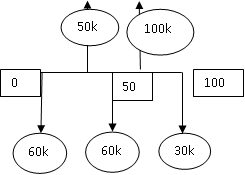
If=r=-60kg-60kg-30kg+50=-100kg
E=100kg
IMA=60(0)-50(20)+60(50)+30(!00)=0-1000+2000+3000=5000kg
5000kg.cm=100(x)
X=5000/100=50 cm de A
IMA=60(0)-50(20)-100(50)+60(50)+30(100)=
0-1000-5000+3000+3000=-6000+6000
0=0
Equilibrio rotacional
Compre una cuerda para colgar 2 macetas en mi jardín el proveedor me comento que la cuerda tiene una resistencia de 250 N. sobre una viga que casi no pesa cuelgo 2 macetas de 200N y 60N como se muestra la figura.
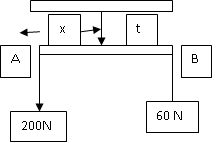
Si T>250 se rompe
Si T<250 resiste
IF=-200+ T-60=0
T=200+60
T=260
IMA=(200)(0)-260(x)+60(10)=0-260x+600=0
260x=600
X=600/260
X=2.50m
Equilibrio traslacional
Una pelota de 100N suspendida por una cuerda A es tirada hacia un lado en forma horizontal mediante otra cuerda B y sostenida de tal manera que la cuerda A forma un ángulo de 30 grados con el muro vertical como se muestra en la figura.
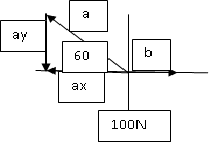
Sen 60=100/A
A sen 60=100
A=100/sen 60=100/0.8660=115.74
Cos 60=b/a=b/115.74
B=(115.74)(0.5)=57.73N
